勾股定理计算器
勾股定理
对于直角三角形:斜边 (c) 的平方值等于腿 (a) 的平方值和腿 (b) 的平方值之和:
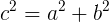
斜边 (c) 计算
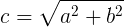
直边(a)计算
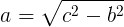
直边 (b) 计算

什么是勾股定理?
勾股定理描述了直角三角形的三条边在欧几里得几何中是如何相关的。它指出直角三角形边的平方和等于斜边的平方。你也可以把这个定理看作是斜边公式。如果直角三角形的边是 和,斜边是 ,则公式为abc
a² + b² = c²
该定理归功于生活在公元前六世纪的古希腊哲学家和数学家毕达哥拉斯。虽然它以前被印第安人和巴比伦人使用,但毕达哥拉斯(或他的学生)被认为是第一个证明这个定理的人。应该指出的是,没有具体证据表明毕达哥拉斯本人研究或证明了这个定理。
如何使用勾股定理
-
将两个长度输入到公式中。例如,假设您知道,并且我们想要找到斜边的长度。
a = 4b = 8c -
将值放入公式后,我们有
4²+ 8² = c² -
将每个术语平方以获得
16 + 64 = c² -
组合类似的术语以获得
80 = c² -
取等式两边的平方根得到 。继续使用我们的毕达哥拉斯定理计算器进行检查!
c = 8.94
请注意,如果要求解 a 或 b,则在组合类似项并取平方根之前,请重新排列方程以隔离所需的变量
毕达哥拉斯定理计算器将以我们上面显示的相同方式求解边。我们提供了一种方法,向您展示如何解决您的问题,如果您更喜欢手工完成。
什么是斜边公式?
斜边公式只是取勾股定理并求解斜边。求解斜边,我们只需取等式两边的平方根并求解 。当这样做时,我们得到.这只是勾股定理的扩展,通常与斜边公式的名称无关。ca² + b² = c²cc = √(a² + b²)
处理三角形时的其他注意事项
请注意,三角形的边具有一定程度的梯度或斜率。我们可以使用斜率计算器来确定每边的斜率。在直角三角形中,形成直角的边将具有乘积为 -1 的斜率。如果您希望手动计算,则斜率的公式为
(y₂ - y₁)/(x₂ - x₁)
因此,如果坐标为 ,则线段的斜率为 。如果形成角度的另一段的斜率为,则线将垂直,因为 。因此,三角形是直角三角形。(3,6) and (7,10)(10-6)/(7-3) = 1-11 * -1 = -1
您还可以使用直角三角形计算器计算出直角三角形的缺失边长和角度。如果问题中给出的角度以度为单位,并且您想要转换为弧度或弧度到度,请查看我们的角度转换器。有一种简单的方法可以将度转换为弧度,将弧度转换为度。
如果角度以弧度为单位
-
乘以
180/π
如果角度以度为单位
-
乘以
π/180
有时您可能会遇到缺少两个或所有三个边长的问题。在这种情况下,毕达哥拉斯定理计算器将无济于事 - 您将使用三角函数来求解这些缺失的部分。